Description

NNSFν is a python package that can be used to compute neutrino structure functions at all momentum transfer energies in the inelastic regime. It relies on Yadism for the description of the medium- and large-\(Q^2\) regions while the low-\(Q^2\) regime is modelled in terms of a Neural Network (NN).

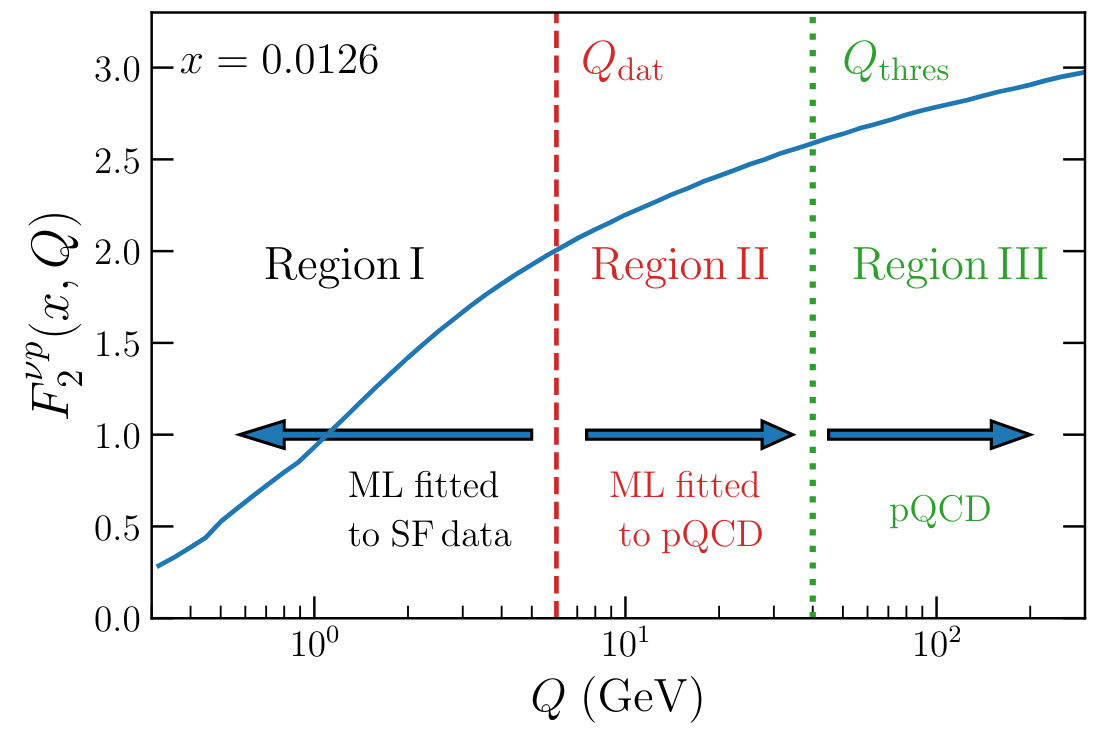
In the low- and intermediate-\(Q^2\) regions the parametrisation of the neural network structure functions with their associated uncertainties are constructed by training a machine learning model to available experimental data. That is, given an observable \(\mathcal{O}\) that is defined as a linear combination of structure functions:

\[\mathcal{O} = N \left( C_1 F_2^{\nu} + C_2 F_2^{\bar{\nu}} + C_3 F_L^{\nu} + C_4 F_L^{\bar{\nu}} + C_5 x F_3^{\nu} + C_6 x F_3^{\bar{\nu}} \right),\]

we fit the structure functions \(F_i^{k} \equiv F_i^{k} \left( x, Q^2, A \right)\) for \(i=2, 3, L\) and \(k =\nu, \bar{\nu}\). It should be noted that for \(i = 3\) we actually fit \(xF_3\) instead of \(F_3\). The coefficients \(C_j\) which depend on \((x, Q^2, y)\) are also computed using Yadism and they have to match data point per data point to the experimental datasets while the normalisation \(N\) depends on how the observable is measured experimentally.

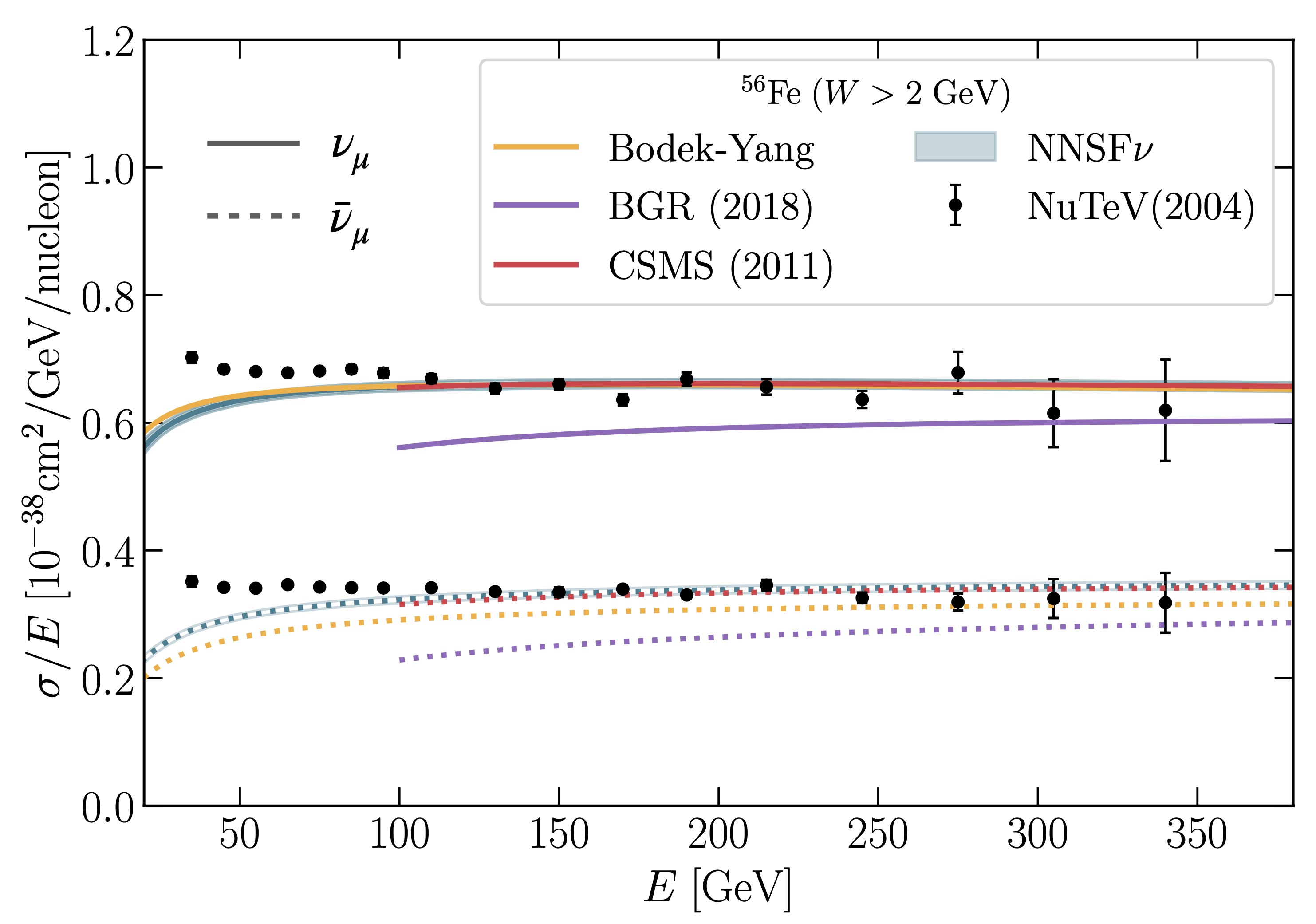
The resulting predictions from NNSFν are also made available in terms of fast interpolation LHAPDF grids that can be accessed through an independent driver code and directly interfaced to the GENIE Monte Carlo event generator.